4-я лекция, 2010.

 29.09.10.

3б. ГИДРОСТАТИКА (продолжение 3-й темы-лекции)

 3.5. Сила давления жидкости на криволинейные стенки.

Плавание тел.

3.6 Сила давления жидкости па плоскую стенку

3.7. Прямолинейное равноускоренное движение сосуда с жидкостью.

3.8. Равномерное вращение сосуда с жидкостью

3.5. Сила давления жидкости па плоскую стенку

Давление жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом, определяется по  основному уравнению гидростатики

Р=Р₀+hρg

Определим силу F давления, действующую со стороны жидкости, на участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.

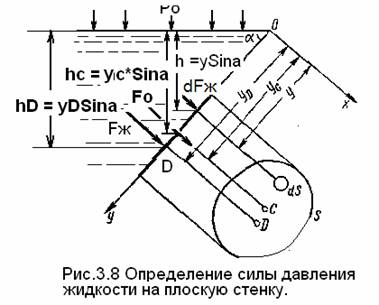
Ось Ох направим перпендикулярно плоскости стенки от точки ее пересечения со свободной поверхностью жидкости, а ось Оу — перпендикулярно оси Ох в  плоскости стенки.

Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS (давление действующее в точке, одинаково для произвольно расположенной площадки)

dFж = P*dS =(P₀ + ρhg)dS = P₀*dS + ρhg*dS,

где Р₀ — давление на свободной поверхности, h — глубина расположения площадки  dS.  Для определения полной силы Fж проинтегрируем полученное выражение по всей площади S:

,

где у — координата площадки dS, h = у*Sinα .

Последний интеграл  представляет собой статический момент площади S относительно оси Ох и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.

Следовательно,

Fж = P₀S+ρg(y_c Sinα) S = P₀S+ρgh_cS    (3.11)

здесь h_c = (Sinα)y_c — глубина расположения центра тяжести площади S, или

Fж = ρg (H₀ +h_c)S = P_cS,                     (3.12)

Полная сила давления жидкости Fж на плоскую стенку равна произведению площади стенки S  на гидростатическое давление Р_с в центре тяжести этой площади.

1.В частном случае, когда давление Р₀ является атмосферным и действует также с другой стороны стенки, сила F_{изб ж} избыточного давления жидкости на плоскую стенку равна лишь силе Fж давления от веса жидкости, т. е.

Fизб ж =Fж = P_cS= ρgh_cS.

2. В общем случае давление Р₀ может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку 6удем рассматривать как сумму двух сил: F₀ от внешнего давления Р₀ и силы Fж   от веса жидкости, т. е.

F= F₀ + Fж = (P₀+Pс)S.        (3.13.)

Рассмотрим  вопрос о точках приложения этих сил, называемых центрами давления*.

Так  как внешнее давление Р₀ передается всем точкам площади S одинаково, то его равнодействующая F₀ будет приложена в центре ус тяжести площади S.

Для нахождения точки приложения силы давления Fж от веса жидкости (точка D) применим теорему механики согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, т. е.

где у_D — координата точки приложения силы.

Ранее уже было найдено выражение для силы от веса жидкости действующей на плоскую стенку, это выражение (3.11):  F_ж = ρgh_D*S = ρg(y_сSinα)*S  и dF_ж= ρgh*dS= ρg(ySinα)*dS. Используя  y_с и у, получаем 

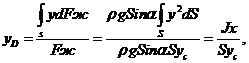        (3.14)

где  - момент инерции площади S относительно оси Оx.

Учитывая, что

Jx = Jx₀+y_c²S,                    (3.15)

Jx₀  - момент инерции площади S относительно центральной оси, параллельной оси Ох), находим

у_D = у_с+ J_x0/(у_сS),                                  (3.16.)

Таким образом, точка приложения силы F_ж расположена ниже центра тяжести площади стенки; расстояние между ними

Δу = J_x0/( у_сS),                 (3.17) .

Если давление Р₀ равно атмосферному, то точка D и будет центром давления.

При Р₀ выше атмосферного центр давления находят по правилам механики, как точку прило-жения равнодействующей двух сил F₀ и F_ж ,  чем больше первая сила по сравнению со второй  тем, очевидно, центр давления ближе к центру тяжести площади S.

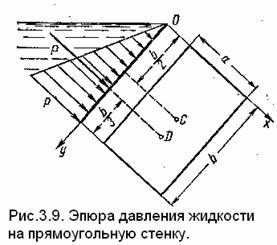
В частном случае,  когда стенка имеет форму прямоугольника размерами а × b (рис. 3.9) и одна из его сторон  а  лежит на свободной поверхности с атмосферным давлением, центр давления D находится па расстоянии b/3 от нижней стороны.

Ранее указывалось, что в жидкостях возможны лишь распределенные силы. Поэтому центры давления можно рассматривать лишь условно.

3.6. Сила давления жидкости на криволинейные стенки.

Плавание тел.

Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов. Чаще всего рассматривают цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.

Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной к плоскости чертежа (рис.3.10), и определим силу давления жидкости на эту поверхность в двух случаях: жидкость расположена сверху (рис. 3.10а); жидкость расположена снизу (рис. 3.10б).

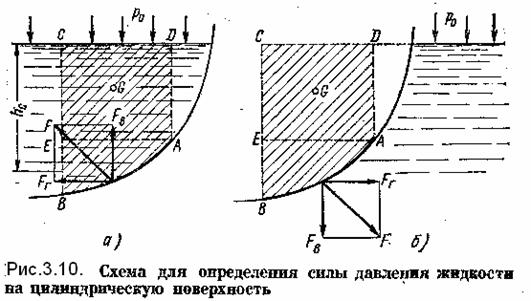
В первом случае выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем АВСD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях. Если жидкость действует на стенку АВ с силой F, то стенка АВ действует на жидкость с силой F, направленной в обратную сторону. На рис. 3.10 показана эта сила реакции, разложенная на две составляющие: горизонтальную F_г и вертикальную F_в.

Условие равновесия объема АВСD в вертикальном направлении имеет вид

F_в = Р₀S_г + G ,                      (3.18)

где Р₀ давление на свободной поверхности жидкости; S_г — площадь горизон- тальной проекции поверхности АВ; G — вес выделенного объема жидкости.

Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости па поверхности ЕС и АВ взаимно уравновешиваются и остается лишь сила давления на площадь ВЕ т. е. на вертикальную проекцию поверхности АВ –Sв. Тогда

F_г= S_вρgh_c+ Р₀S_в = S_в(ρgh_c+ Р₀).            (3.19)

Определив по формулам (1.31) и (1.32) вертикальную и горизонтальную составляющие полной силы давления F, найдем

.               (3.20)

Когда жидкость расположена снизу (рис.3.10), гидростатическое давление во всех точках поверхности АВ имеет nе же значения, что и в первом случае, но направление его будет противоположным, и суммарные силы Fв и Fг определятся теми же формулами (3.18)  и (3/19), но с обратным знаком. При этом под величиной G следует понимать так же, как и в первом случае вес жидкости в объеме АВСD, хотя этот объем и не заполнен жидкостью.

Положение центра давления на  цилиндрической стенке можно легко найти, если известны силы Fв и Fг и определены центр давления на вертикальной проекции стенки и центр тяжести выделенного объема АВСD.

Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность является круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элементарная сила давления нормальна к поверхности, т. е. направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические поверхности применим и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

Описанный выше прием нахождения вертикальной составляющей силы давления жидкости па криволинейную стенку используют для доказательства закона Архимеда.

Пусть в жидкость погружено тело произвольной формы объемом V (рис. 3.11).

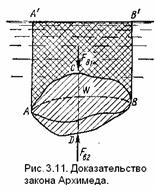
Спроектируем его на свободную поверхность жидкости и проведем проек-тирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АСВ от нижней ее части ADB.  Вертикальная составляющая F_в1 силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме АА’BВ’CA. Вертикальная составляющая F_в2 силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме АА’В’BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.

F_А = F_в2  - F_в1  = G_ACBD =Vρg.                     (3.21)

В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила направленная вертикально вверх, численно равная весу жидкости вытесненной телом и приложенная в центре тяжести объема погруженной части тел.

Сила F_А называется архимедовой силой, или силой поддержания, а точка ее приложения, т. е. центр тяжести объема V — центром водоизмещения.

В зависимости от соотношения веса G тела и архимедовой силы возможны три случая: 1) G> F_А — тело тонет; 2) G<F_А — тело всплывает и плавает на поверхности жидкости в частично погруженном состоянии; 3) G = F_А тело плавает в полностью погруженном состоянии.

Для равновесия плавающего тела, кроме равенства G = F_А  должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии,  заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения. Устойчивость равновесия тел плавающих на поверхности жидкости здесь не рассматривается.

3.7. Прямолинейное равноускоренное движение

сосуда с жидкостью.

При движении сосуда на частицы жидкости, кроме сил тяжести действуют еще силы инерции,  под действием этих сил жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Относительным покоем называется равновесие жидкости в  движущемся сосуде, находящейся под действием сил тяжести и инерции.

При относительном покое положение свободной поверхности и поверхностей уровня,  отличается от их положения для жидкости в неподвижном сосуде.

Для определения формы и положения этих поверхности учитывается основное свойство поверхности уровня.

Поверхности уровня – это поверхности равного давления.

Основное свойство поверхностей уровня  -  равнодействующая массовых сил всегда нормальна  к этим поверхностям.

Пользуясь полным дифференциалом давления  dР

dP=ρ(X*dх+У*dy+Z*dz),          (3.22)

рассмотрим взаимодействие сил при относительном покое жидкости в сосуде.

Так как вдоль поверхности уровня  dР=0,

X*dх+У*dy+Z*dz = 0          (3.22'),

в результате получаем уравнение поверхности равного давления. Трехчлен (3.22') определяет работу сил на перемещениях dх, dy, dz. В данном случае перемещение взято по поверхности равного давления, так как dР=0. И из этого выражения следует, что  работа массовых сил вдоль поверхности равного давления равна нулю. Это значит, что в состоянии относительного покоя результирующее ускорение перпендикулярно к  соответсвующему элементу поверхности равного давления.

Первый случай:   сосуд, движущийся прямолинейно и равноускоренно;

Второй случай: сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.

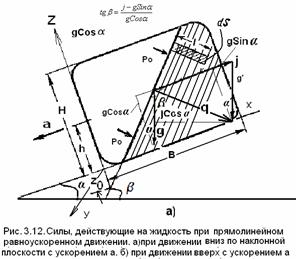
На рис.3.12 изображен сосуд, движущийся вниз с ускорением а по плоскости наклонённой под углом  α   к горизонту. Оси координат оси координат связаны с движущимся телом.  Единичная массовая сила инерции равна ускорению а и направлена в противоположную сторону (з-н Ньютона).

1. Пусть на жидкость действует  суммарная массовая сила F, проекции которой Fx, Fy, Fz , поделенные на  массу: Fx/m  являются проекциями единичной массовой силы на оси Ох, Оу, Oz:  Х, У и Z.

F = Fx+Fy+Fz = mа,  F/m = Fx/m +Fy/m +Fz/m = X +Y + Z = а.

Все выделенные составляющие являются векторными величинами.

 Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны произведениям проекций единичных сил, умноженным на массу выделенного объема.

Fx = mX,               Fy = mY,                     Fz = mZ.

Результирующую единичную массовую силу, действующую на жидкость,  найдем как сумму единичных векторов силы инерции j  и силы тяжести g, при этом единичная сила инерции Fи = j = - a направлена в сторону  противоположную ускорению а (рис.3.12).

Проекции сумм массовых сил на оси

          Ox: X = j - gSinα,   

         Oz : Z = -gCosα,

Оx: Y = 0.

 

Подставляя эти выражения в выражение для дифференциала, получим

(1/ρ)dp = [(j - gSinα)dx – (gCosα)dz],

после интегрирования

p = ρ [(j - gSinα) x – (gCosα)z +С,  (3.21)

полагая Р – const,  получаем уравнение изобарических поверхностей, к

С + Р(const) = С₁ .

ρ [(j - gSina) x – ρgCosa* z +С₁ = 0 (3.22)

Это уравнение дает семейство плоскостей, параллельных оси у. Одной из них является свободная поверхность. Обозначим через z₀ координату пересечения свободной поверхности с осью z. Подставив в формулу (3.22) х₀ = 0, z = z₀, находим С₁=ρg z₀Cosα для свободной поверхности. Уравнение этой поверхности имеет вид

   (3.23)

где коэффициент в линейном уравнении равен тангенсу угла β

      (3.24)

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно   и   равноускоренно к уравнению (3.23) нужно добавить уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень h.

Если сосуд движется без трения только под действием силы тяжести, то j= gSinα β = 0, то есть свободная поверхность параллельна  плоскости движения. Полагая в

формуле (3.21) х = 0, z = z₀, P = P₀, получим C = P₀+ (ρgCosa)z₀. Формула для определения давления в любой точке жидкости, находящейся в относительном покое при прямолинейном движении

Р = P₀+ρ(j-gSina)x+ρgCosa(z₀ – z).   (3.25)

Можно также использовать суммарную массовую единичную силу q.

Возьмем на рис.3.11 около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический  объем с образующей, нормальной к  свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

РdS = P₀dS + q(ρldS),

где последний член представляет собой полную массовую силу q – суммарная единичная массовая сила, действующая на выделенный объем жидкости массой М= ρldS– масса, а l — расстояние от точки М до свободной поверхности.

После сокращения на dS получим

Р = P₀ + qρl,                          (3.26)

3.8. Равномерное вращение сосуда с жидкостью

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью ω  вокруг его вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее изменится.

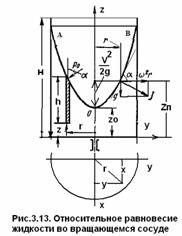
В центральной части уровень жидкости опустится, у стенок  она поднимется, и вся свободная поверхность жидкости станет поверхностью вращения (рис.3.13).

На жидкость будут действовать две массовые силы: единичная сила тяжести F_g = g и единичная центробежная сила Fцб = ω²r.

Проекции этих сил на оси координат дадут следующие выражения

X = (V²/r) Cos(r^x) = ω²r Cos(r^x)= ω²X

Y = (V²/r) Cos(r^y) = ω²r Cos(r^x)= ω²Y,   Z = -g

 

Подставляя это выражение в выражение  для дифференциала давления

dp  = ρ(Xdx  +  Ydy + Zdz),    

Получим

dp  = ρω² (Xdx  + Ydy) –ρ gdz,

вынеся знак дифференциала за скобки, получим

dp  = ρ(ω²/2)d(X²  + Y²) –ρ gdz,

после интегрирования получим выражение для определения давления в любой точке

 p  = ρ(ω²/2) (X²  + Y²) –ρ gz + С,

полагая в этом выражении Р – const, получаем уравнение изобарических поверхностей

ρ(ω²/2) (X²  + Y²) – ρgz + С₁ = 0.

Это будут конгруэнтные параболоиды вращения  с осью Oz. Один из этих параболоидов – свободная поверхность жидкости.

Обозначив через z₀ координату вершины параболоида свободной поверхности, получим x = y = 0, откуда С₁ = ρgz₀,  

                           ρ(ω²/2) (X²  + Y²) – ρgz + ρgz₀  = 0

 и уравнение поверхностей уровня свободной поверхности получит вид

Z –Z₀ = (ω²/2) (x²  + y²).                    (3.27)

Уравнение свободной поверхности получит вид

Z_П –Z₀ .                                  (3.28)

Если внешнее давление равно Р₀ то, задав в уравнении для давления Р = Р₀, x=y=0, z = z₀ , находим постоянную С = Р₀ + ρg z_0. Тогда закон распределения давления выразится формулой

P               (3.29)

Пользуясь этими уравнениями  можно определить положение свободной поверхности в сосуде, максимальную высоту Н подъема жидкости и высоту z_{0 =} h  расположения вершины параболоида при данной угловой скорости ω.  Для этого необходимо использовать еще уравнение объемов: объем неподвижной жидкости равен её объему во время вращения.

На практике часто рассматривается вращение сосуда с жидкостью, когда угловая скорость ω столь велика, что силой тяжести можно пренебречь по сравнению с центробежными силами. При этом закон изменения давления в жидкости легко получить из формулы (3.29),  в которой следует принять g(z₀ - z) = 0.

Поверхности уровня примут вид цилиндров с общей осью  -   осью вращения сосуда. Если сосуд не был заполнен перед началом вращения,  давление Р₀ будет действовать не в центре, а при r = r₀,  вместо выражения (3.29) будем иметь

Р = Р₀ + ρ ω² (r —r²)/2g,                          (3.30)

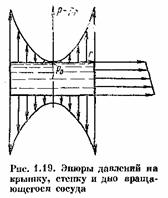
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси вращения (или на кольцевую часть этой стенки).

Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr;

dF = рdS = [Р₀ + ρ ω² (r² - r₀² )/2] 2πrdr,

а затем выполнить интегрирование в требуемых пределах.

При большой угловой скорости жидкости можно получить весьма значительную суммарную силу давления на стенку. Этот эффект используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил нормального давления. Способ, указанный выше,  применяют для определения силы осевого давления жидкости на рабочие колеса центробежных насосов, а также на крышки центрифуг.