11. Расчет резьбовых соединений, нагруженных предварительной силой затяжки и последующей осевой силой.

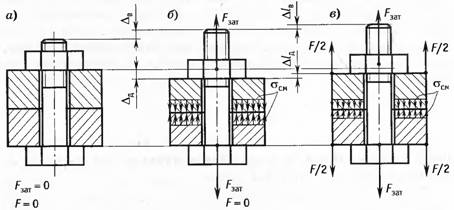
Под действием силы затяжки F_зат винт удли­нится на величину Δ_в, а детали сожмутся на величину Δ_д. Ве­личины деформаций Δ_в и Δ_д в общем случае не равны и зависят от податливостей винта λ_в и деталей λ_д

После приложения к деталям внешней силы F винт дополнительно удлинится на величину Δl_в, и на столь­ко же уменьшится сжатие деталей Δl_д,

Так как податливости деформируемой части винта Δ_в и де­талей Δ_д различны, сила F при одинаковой деформации рас­пределится между ними обратно пропорционально их величи­нам. Если часть силы, дополнительно нагружающую винт, обозначить через χF, то остальная часть, равная (1-χ)F идет на разгрузку сжатых деталей.

Отсюда получим выражение коэффициента основной на­грузки:

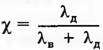
При соединении стальных деталей стальным винтом коэф­фициент χ принимает значения 0,2...0,3. При отсутствии внешней нагрузки F сила, растягивающая винт, и сила, сжимающая детали, равны между собой и равны силе затяжки. После приложения внешней нагрузки F сила, растягивающая винт, увеличивается, а сила, сжимающая де­тали, уменьшается. Если увеличение силы на винте обозна­чить ΔF, то

Остаточная сила, сжимающая детали составит

Расчетную силу, действующую на винт, находят как сумму сил от затяжки и доли всех внешних сил, определяемую коэф­фициентом χ:

.

 

12. Расчет резьбовых соединений, нагруженных отрывающей силой и опрокидывающим моментом.

Допущения: 1) расчет сводится к нахождению наиболее нагруженного винта 2) кронштейн под действием момента поворачивается относительно оси, проходящей через точку C, как абсолютно твердое тело, деформируются только зоны вблизи винта 3) контактные напряжения на стыке от сил и моментов пропорциональны перемещениям основания, т.е. вдоль оси y меняются линейно.

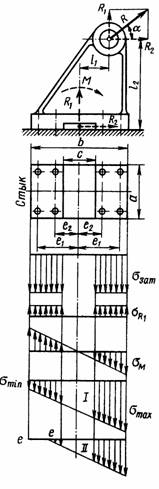
Нераскрытие стыка:

Если неравенство решить относительно σ₀, и ввести коэффициент плотности стыка υ=1,5-3, то . Из этого условия находят:

, где z – число винтов, A_д – площадь поверхности стыка.

, где , в итоге получаем:

После подсчета силы затяжки находят наиболее нагруженный винт, при этом считают, что сила затяжки о отрывающая сила действуют одинаково, а момент нет, следовательно, самый нагруженный винт будет слева от центра кронштейна.

Запишем условие равновесия:  .

С учетом допущений .

, тогда расчетная сила, действующая на эти винты, находится как .

На кронштейн также действует сдвигающая сила F₂. Кронштейн не сдвинется с места, если сила трения в основании окажется выше сдвигающей силы.

, где f – коэффициент трения. Момент в этом уравнении не учли, так как он не влияет на величину силы трения, ибо справа он линейно увеличивает нормальную силу, а слева линейно уменьшает.

 

13. Материалы резьбовых соединений и допускаемые напряжения.

1) углеродистые стали (для легко нагруженных деталей), легированные стали (для тяжелого нагружения)

2) Спецстали (жаропрочные, работающие в агрессивных средах, вакууме)

3) Цветные сплавы (латунь, бронза, дуралюмин)

Согласно ГОСТ 17594-87 существует 12 классов прочности резьбовых деталей.

Если класс прочности 4.6, то σ_в=4*100 МПа, σ_т=4*6*10 МПа

Если класс прочности 5.8, то σ_в=5*100 МПа, σ_т=5*8*10 МПа

Допускаемые напряжения при статическом нагружении:

1) растяжение

 

S – коэффициент запаса, при точном расчете и контролируемой затяжке 1.2…1.5.

Меньшие значения для резьб большого диаметра и наоборот.

2) кручение (срез)