44. Особенности расчета косозубых и шевронных колес на сопротивление контактной и изгибной усталости. Чем обуславливается повышение нагрузочной способности косозубых и шевронных передач по сравнению с прямозубыми.

Контактная усталость:

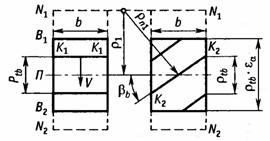
В косозубых и шевронных передачах зубья входят в зацепление постепенно. Расчет проводят с учетом геометрии в сечении, нормальном к направлению зуба. Результирующая сила в нормальной плоскости на делительной окружности . Суммарная длина контактных линий , . Радиус кривизны эвольвенты в полюсе зацепления в нормальном сечении .

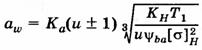
Ψ_ab – коэффициент относительной ширины колеса, K_H – коэффициент нагрузки. Условие контактной прочности , максимальное расчетное напряжение , T_1П – максимальный вращающий момент на шестерне, T₁ – вращающий момент на шестерне, принятый при расчетах на выносливость при изгибе.

На изгибную усталость:

Для косозубых и шевронных передач характерно повышенное сопротивление усталости при изгибе.

 - коэффициент, учитывающий торцевое перекрытие.

 - коэффициент, учитывающий наклон зуба, получен экспериментально.  - коэффициент осевого перекрытия.

Прочность зубьев при однократной нагрузке .

Максимальные расчетные напряжения , T_max – максимальный вращающий момент на шестерне, T – вращающий момент на шестерне, принятый при расчетах на выносливость при изгибе.

 

45. Конические зубчатые передачи, достоинства и недостатки, Область применения. Типы зубчатых колес, основные геометрические параметры конического зубчатого колеса. Передаточное число конической зубчатой передачи.

Конические зубчатые передачи передают механическую энер­гию между валами с пересекающимися осями. Несмотря на сложность изготовления и монтажа, конические передачи получили ши­рокое распространение в редукторах общего назначения, в металлообраба­тывающих станках, вертолетах, авто­мобилях. (Это достоинства).

Недостатки: 1) необходимость регулировки передачи 2) меньшая нагрузочная способность 3) сложность изготовления и более высокие точности 4) большие осевые нагрузки.

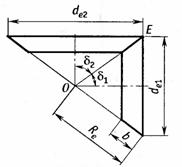
Зацепление двух конических ко­лес можно представить как качение без скольжения конусов с углами при вершинах 2δ₁ и 2δ₂. Эти конусы назы­вают начальными. Линию касания этих конусов ОЕ называют полюсной линией или мгновенной осью в отно­сительном вращении колес. Основное

применение получили передачи ортогональные с суммарным углом между осями δ₁+ δ₂ = 90°. Конические зубчатые переда­чи выполняют без смещения исходного контура (x₁ = 0, х₂=0) или равносмещенными (х₂=-х₁). Поэтому начальные конусы совпадают с делительными.

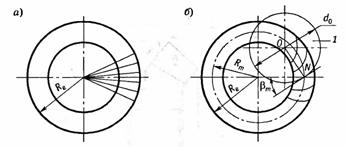
Конические колеса обычно выполняют прямозубыми или с круговыми зубьями Прямозубые пе­редачи в основном применяют при окружных скоростях до 3 м/с, при более высоких скоростях применяют передачи с круговыми зубьями. Конические колеса с косыми зубьями применяют весьма редко из-за сложности изготовления и контроля.

Основные геометрические параметры.

К основным отно­сятся следующие геометрические параметры конических зуб­чатых колес.

Углы, делительных конусов связаны с их диаметрами (и числами зубьев z).

Модуль конического колеса меняется по длине зуба. За ос­новной принимают окружной модуль на внешнем торце m_te, который удобно измерять. Внешние делительные диаметры колес равны

Внешнее конусное расстояние

Конусное расстояние до середины зуба

, где  - коэффициент ширины зубчатого венца.

Средний делительный диаметр и модуль находят из подобных треугольников

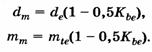
Диаметр вершин зубьев

При расчете на прочность конические колеса заменяют на равнопрочные им цилиндрические колеса. Диаметр эквивалентного зубчатого колеса равен

.

Эквивалентное число зубьев из зависимости  равно

.

Для передач с круговыми зубьями приводят еще косозубое колесо к прямозубому

Понижающие конические передачи можно выполнять с передаточным отношением u=1…10. Обычно u<6. Повышающие передачи имеют u не более 3. Большие передаточные отношения усложняют конструирование шестерни и ее опор. Число зубьев колеса .