99) Особенности определения осевых сил, нагружающих радиально-упорные подшипники качения. Минимальные осевые силы для радиально-упорных регулируемых подшипников качения. Как определить осевые реакции в опорах с учетом этих сил.

Обычно вал устанавливают на двух опорах. При применении в опорах радиально-упорных подшипников нерегулируемых типов внешнюю осевую силу воспринимает тот подшипник, который ограничивает осевое перемещение вала под действием этой силы. При определении осевых нагрузок, воздействующих на радиально-упорный подшипник регулируемых типов, следует учитывать осевые силы возникающие под действием радиальных нагрузок из-за наклона контактных площадок. Значения этих сил зависят от типа подшипника, угла контакта, значений радиальных сил, а также от того как отрегулирован подшипник.

Подшипник регулируют так, чтобы осевой зазор при установившемся температурном режиме был бы близок к 0. В этом случае под действием радиальной нагрузки F_r находится около половины тел качения, а суммарная осевая составляющая из-за наклона контактных площадок равна e’F_r, где e’=e для радиально-упорного подшипника при α>=18°, e’=f(F­r/C_0r) для радиально-упорных шариковых подшипников с малыми номинальными углами контакта (α<18°).

Таким образом e’F_r представляет собой минимальную осевую силу, которая должна действовать на радиально упорный подшипник при заданной радиальной силе F_r: F_{a min} = e’F_r.

Для обеспечения нормальных условий работы осевая сила, нагружающая подшипник должна быть не меньше минимальной: F_a>=F_{a min}.

Нахождение осевых реакций опор.

F_A , F_R -  внешние осевая и радиальная нагрузка действующая на вал; F_r1 , F_r2 – радиальные реакции опор; F_a1 , F_a2 – осевые реакции опор с шариковыми радиально-упорными подшипниками.

В соответствии с консольным нагружением силой F_R: F_r1>F_r2. При одинаковых подшипниках в опорах (F_r1/C_or)> (F_r2/C_or) и e’₁>e’₂ => e’₁F_r1> e’₂F_r2.

Решение будет найдено, если:

1)     из F_a>=F_{a min} => F_a1>=e’₁F_r1, F_a2>=e’₂F_r2

2)     из условий равновесия вала под действием осевых сил следует: F_A+F_a1-F_a2=0.

Осевую силу в одной из опор примем равной минимуму, пусть например F_a1=e’₁F_r1, тогда из условия равновесия вала F_a2= F_A+F_a1= F_A+ e’₁F_r1.

Проверим выполнение условия F_a>=F_{a min} для второй опоры. Действительно: F_a2>e’₂F_r2. Следовательно осевые силы найдены правильно.

 

100) Почему целесообразно конструировать опоры так, чтобы кольцо, вращающееся относительно нагрузки было установлено с натягом.

Кольцо с местным нагружением устанавливают с зазором или небольшим натягом, т.к. обкатывания в этом случае не происходит. Кроме того это важно для обеспечения осевых перемещений колец при монтаже и при температурной деформации валов и корпусов. Поле допуска посадочного отверстия подшипника смещено внутрь отверстия, а поле допуска посадочного диаметра наружного кольца смещено «в тело». При таком расположении полей допусков легче обеспечить натяг на валу.

 

101) Как изменится расчетный ресурс шарикового подшипника, воспринимающего постоянную радиальную нагрузку, если вращение внутреннего кольца заменить вращением наружного кольца с той же частотой.

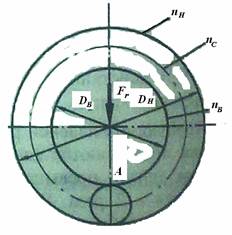
С кинематической точки зрения подшипники можно рассматривать как планетарный механизм, в котором роль водила выполняет сепаратор, а тела качения являются сателлитами.

В соответствии с теоремой Виллиса:

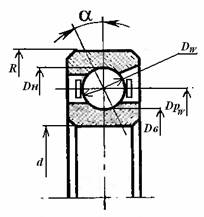
Где n_В, n_Н, n_С – частоты вращения соответственно внутреннего кольца, наружного кольца и сепаратора. D_Н , D_В – соответственно диаметры окружностей расположения точек контактов тел качения на наружном и внутреннем кольцах. Учитывая что  находим частоту вращения сепаратора:

 где f_g=(D_w/D_Pw)*cosα – геометрический параметр.

Если внутреннее кольцо подвешено (n_В=0), то за один оборот сепаратора наиболее нагруженная точка А на внутреннем кольце получает число циклов нагружения, равное числу тел качения z. За один оборот наружного колеса сепаратор делает (1+ f_g)/2 оборота и число циклов нагружения точки А: (1+ f_g)*z/2. Следовательно в течение L миллионов оборотов наружного кольца число циклов повторных нагружений точки А составляет .

При неподвижном наружном кольце n_c=(1- f_g)*n_B/2.

Сепаратор  вращается в ту же сторону что и внутреннее кольцо и за один оборот внутреннего кольца сепаратор поворачивается на (1-f_g)/2 оборота. Точка А получает  циклов нагружения. В течение L миллионов оборотов внутреннего кольца число циклов повторных нагружений точки А .

 

 

Все что связано с ресурсом L смотреть в 89!