Содержание курса:
1)Свойства жидкостей;
2)Гидростатика;
3)Кинематика жидкостей;
4)Гидродинамика;
5)Основы теории лопастных насосов;
6)Основные сведения об объемных гидроприводах.
1-я лекция,
Основные вопросы к зачету по этой лекции:
1.1 Введение. Исторические сведения о гидравлике.
1.2.Предмет и задачи технической гидромеханики (гидравлики).
1.3. Силы, действующие на жидкость.
Давление жидкости.
1.4. Примеры гидравлических систем.
Рекомендуемая литература
1.1 Введение.
Исторические сведения о гидравлике.
Гидравликой
называется прикладной раздел механики, изучающий законы равновесия и движения
жидкостей для решения технических задач.
Гидравлика зародилась в цивилизациях Древнего мира при создании систем водоснабжения и канализации. Такие системы были обнаружены при раскопках Кносского дворца на острове Крит. Они были построены за 2000 лет до нашей эры.
Один из виднейших гидравликов древнего мира - греческий ученый Архимед, живший в третьем столетии до нашей эры, известен открытием закона плавания тел и изобретением винтового насоса.
Архимед выполнял задание царя Гирона по определению состава короны, у царя было сомнение, что в составе сплава много серебра. Удельный вес золота и серебра был известен, но корона имела неправильную форму и ее объем определить было затруднительно. Архимед погрузил в воду серебряный и золотой бруски равные по весу короне, затем корону. Воды из емкости выплеснулось меньше, чем от серебряного бруска, но больше, чем от золотого. Утверждают, что так был открыт основной закон гидростатики: закон Архимеда.
Закон Архимеда: на тело, погруженное в жидкость или газ,
действует выталкивающая сила, равная весу того количества жидкости или газа,
которое вытеснено погруженной частью тела.
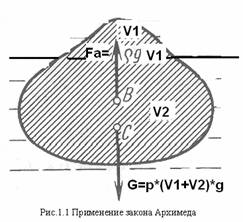
Объем выступающей части айсберга над поверхностью воды равен V1 =
Решение.
Объем айсберга Vа
=(V1+V2) состоит из
двух частей: наводной части c
объемом V1=
G = ρл(V1+V2)g,
где g = 9,8 м/с2 – ускорение свободного падения.
Выталкивающую силу Fа создает только подводный вытесненный объем V2
Fа = m2g = ρмв V2g.
Так как айсберг плавает, эти силы равны
Gа = Fа
= ρл(V1+V2)g = ρмв V2g.
Проведя необходимые преобразования, получим
V2 = V1 /(1 - ρл
/ ρмв) = 200/(1 – 920/1025) = 200/(1-0,897) =
Объем айсберга составит
Vа =(V1+V2) = 200+1960 =
Масса айсберга равна
Ма = ρл(V1+V2) = 920*2160 =
Техническое применение закона Архимеда: плавание тел, дирижабли, подводные лодки и иные устройства.
Существует три основных разновидности
дирижаблей. Жесткие дирижабли (А), например, Гинденбург» (1936), имеют
внутреннюю раму-скелет. Газ, обеспечивающий подъемную силу, содержится в ряде
емкостей - 1, заключенных внутри ее. Общий объем емкостей доходил до
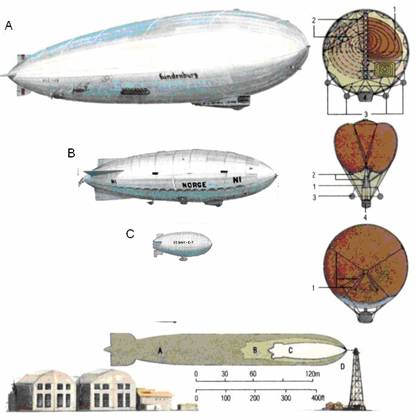
Рис.1.2 Применение закона Архимеда на примере дирижаблей
Емкости с водородом располагались внутри алюминиевого
каркаса -2, на котором были подвешены четыре дизельных двигателя – 3 мощностью по
Полужесткие дирижабли (В), типа «Норвегии» на котором
погиб в Арктике великий полярный исследователь Амудсен при поисках дирижабля
итальянца Нобиле были мало распространены. Хотя у них не было жесткого каркаса
внутри оболочки, от носа до кормы проходил жесткий киль - 1, который служил
опорой для подвески. Оболочка кре-пилась на киле канатами и проволочным
каркасом -2, которые были натянуты поверх нее. Это позволяло сохранить форму
оболочки и поднять все сооружение в воздух. Под килем была закреплена на рамах с кронштейнами
кабина управления -3 и двигатели -4.
Нежесткие дирижабли, или малые (С), имеют гибкую оболочку, форма которой поддерживается за счет надувания под давлением, которое несколько превышает атмосферное. Полезный груз подвешивается при помощи системы веревочного каркаса-1 с целью распределения веса по всей тканевой оболочке. Показанный на рисунке малый дирижабль был создан в 1913г., однако он весьма напоминает те, которые использовались даже во время Второй мировой войны. Аналогичные дирижабли существуют и в наши дни, хотя их немного. Их наполняют негорючим гелием. Сопоставление размеров дирижаблей различных типов(D)показывает, насколько больше может быть дирижабль, если его снабдить жестким каркасом. Другим примером технического применения закона Архимеда является батискаф.
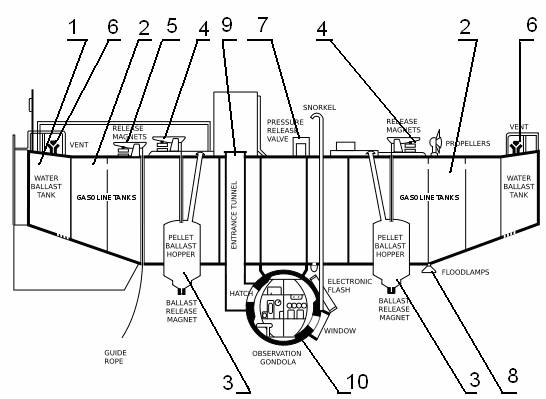
Рис.1.3. Устройство батискафа Триест. 1 – резервуар для водного балласта, 2 – резервуары для бензина, 3- бункер для чугунной дроби, 4 – электромагниты для опорожнения бункеров с чугунной дробью, 5 – электромагниты для заслонок, выпускающих бензин, 6- клапаны продувки и загрузки водного балласта, 7 – клапан сброса давления, 8 – донные прожекторы, 9 – тоннель выхода экипажа, 10 – гондола.
Винтовой
насос или Архимедов винт - водоподъемная машина, вал с винтовой поверхностью, установленный
в наклонной трубе, нижний конец которой погружен в воду. При вращении (напр.,
от ветряного или другого двигателя) винтовая поверхность вала перемещает воду
по трубе на высоте до
Цилиндрическая
труба длиной 4-
Уникальные системы водоснабжения разработали древние инженеры, их акведуки имели многокилометровую протяженность, при этом точно рассчитывались перепады высоты между точками, где были расположены источники воды, и точками, куда вода должна была доставляться по акведукам.
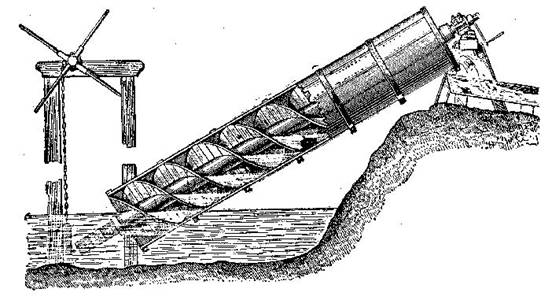
Рис.1.4 Принцип действия винтового насоса.
В Рим
вода поставлялась через 11 акведуков, которые были построены в течение 500 лет
и имели общую длину почти
Самый длинный акведук был построен во втором столетии нашей эры, чтобы поставлять
воду в Карфаген, сейчас это место находится на территории
современного Туниса,
его длина составляла
Римские акведуки были чрезвычайно сложными сооружениями, технологически
они не устарели даже через 1000 лет после падения Римской империи. Римляне
строили их не только в Риме, но и в Галии, и в Испании. Они были построены с
замечательной точностью: акведук в Провансе (современная Франция) имел уклон
Транспортировка воды только за счёт силы тяжести была очень эффективна, через этот акведук проходило 20.000 кубических метров воды в день.
Как наука, гидравлика оформилась при переходе к промышленному производству, это произошло в семнадцатом-восемнадцатом столетии.
Голландский
инженер и математик Симон Стевин написал
книгу, одну из первых по гидростатике. Занимаясь определением силы на плоскую
стенку, он открыл «гидростатический парадокс»: давление
жидкости, определяемое в любой точке сосуда, не зависит от формы сосуда, а
зависит от положения точки относительно уровня свободной поверхности. 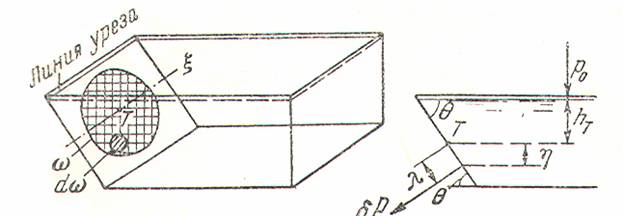
Рис.1.5 Координаты η положительны при отсчете вниз, и отрицательны при отсчете вверх от точки Т.
![]()
![]()
![]()
![]() - второй интеграл,
- второй интеграл, ![]() - статический момент
относительно оси ξ, равен нулю и
Р=Рт*ω.
- статический момент
относительно оси ξ, равен нулю и
Р=Рт*ω.
Стевин вывел формулы для определения усилий на любую часть борта судна, исходя из своего определения «гидростатический парадокса»: давление жидкости, определяемое в любой точке сосуда не зависит от формы сосуда и количества жидкости в нем, а зависит лишь от ее положения относительно уровня свободной поверхности..
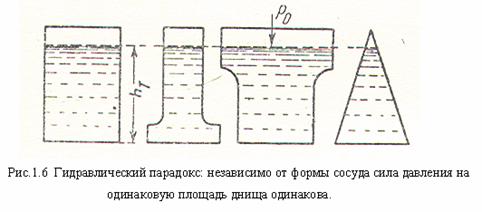
Значение атмосферного давления впервые
экспериментально определил в

Опыт Торричелли заключается в следующем. Стеклянную трубку длиной
около
Давление столба ртути высотой h уравновешивает давление атмосферы. Наблюдения показали, что высота столба ртути в трубке и значение атмосферного давления зависит от погодных условий и от высоты местности.
По постановлению
Парижского парламента от 4 сентября 1624 года было запрещено под страхом
смертной казни «утверждать и преподавать положения, направленные против древних
и признанных авторов". В первую очередь имели в виду Аристотеля, который
среди прочего утверждал, что воздух не имеет веса и что "природа не терпит
пустоты". Торричели - догадался, что всё дело в весе воздуха, а чтобы проверить
идею, заменил воду более плотной жидкостью - ртутью. Он рассуждал так: ртуть
плотнее воды в 13,6 раза, значит, и столб её будет во столько же раз меньше по
высоте. Сегодня его
Наблюдения
показывают, что жидкость, находящаяся в сосуде в состоянии покоя, давит на дно и
стенки сосуда и на любое тело, погруженное в эту жидкость. Давление,
оказываемое покоящейся жидкостью на любую соприкасающуюся с ней поверхность, называют
гидростатическим.
Основной закон гидростатики (закон Паскаля):
«жидкости и газы передают оказываемое на них давление равномерно по всем
направлениям».
Закон сообщающихся сосудов также открыт Паскалем: в сообщающихся сосудах уровни однородных жидкостей (равной плотности), считая от наиболее близкой к поверхности земли точки, равны.
Исаак Ньютон открыл закон трения в жидкости и сформулировал закон сопротивления жидкости движущемуся в ней телу.
Л. Эйлер составил дифференциальные уравнения относительного равновесия и движения жидкости, известные, как уравнения Эйлера и предложил способы описания движения жидкости.
Д.Бернулли получил уравнение невязкой жидкости при установившемся движении, известное как уравнение Бернулли.
В гидравлике получили известность труды француза Навье, создавшего законы движения вязкой жидкости, англичанина Рейнольдса, разработавшего критерии подобия, а также определившего два закона движения жидкости: ламинарный и турбулентный и других.
Русским ученым Н.Е.Жуковским разработана теория гидроудара, открыты важные закономерности в теоретической механике и аэродинамике, также нашим соотечественником Н.П. Петровым разработана гидродинамическая теория смазки.
Гидромеханикой называется наука,
изучающая движение и равновесие жидкостей, а также взаимодействие между
жидкостями и твердыми телами, полностью или частично погруженными в жидкость при
неподвижном состоянии жидкостей или при движении.
Жидкости по молекулярному строению занимают промежуточное положение между твердыми телами и газами, проявляя текучесть, присущую газам и сопротивляемость деформации, присущую твердым тела.
Термину жидкость в гидромеханике часто придают более широкий смысл, чем это принято в обыденной жизни. Жидкими считаются все среды, которым свойственна текучесть т. е. способность сильно изменять свою форму под действием сколь угодно малых сил. Таким образом, в это понятие включают жидкости обычные, называемые капельными и газы - некапельные жидкости.
Капельные жидкости отличаются тем, что в малом количестве под действием поверхностного натяжения принимают сферическую форму, а в большом количестве образуют свободную поверхность раздела с газом. Важной особенностью капельных жидкостей является то, что они мало изменяют свой объем при изменении давления, поэтому их обычно считают несжимаемыми.
Газы могут значительно уменьшаться в объеме под действием давления и неограниченно расширяться при отсутствии давления, т. е. обладают большей сжимаемостью.
Механическое движение этих сред описывается едиными дифференциальными уравнениями.
Однако, решение этих уравнений требует учета специфических свойств упомянутых сред, поэтому механика сплошных сред разделяется на ряд самостоятельных дисциплин: гидромеханику, газодинамику, теорию упругости.
Жидкости и газы с точки зрения механики отличаются только степенью сжимаемости. В условиях, когда это свойство не является определяющим, решения уравнений сплошной среды оказываются одинаковыми для жидкостей и газов.
В зависимости от теоретической или прикладной направленности употребляются наименования теоретическая или прикладная гидромеханика, или техническая гидромеханика, получившая название гидравлики.
В гидравлике рассматривают, главным образом потоки жидкости, ограниченные и направленные твердыми стенками, т. е. течения в открытых и закрытых руслах или каналах. В понятие русло или канал включают поверхности или стенки, которые ограничивают и направляют поток, следовательно, не только русла рек, каналов и лотков, но и различные трубопроводы, насадки, элементы гидромашин и других устройств, внутри которых протекает жидкость.
1.2. Предмет гидравлики
В дальнейшем изложении под термином жидкость будем понимать капельную жидкость, а также газ, когда его можно считать несжимаемым. В гидравлике изучают статику и динамику капельных жидкостей, в основном, рассматриваемых, как несжимаемые.
Законы движения капельных жидкостей и газов при определенных условиях можно считать одинаковыми.
К этим условиям в основном относится малая скорость течения газа.
Внутренние течения газа относятся к области гидравлики в тех случаях, когда их скорости значительно меньше скорости звука и, следовательно, сжимаемостью газа можно пренебречь. Примером такого движения газов являются течение воздуха в вентиляционных системах, в системах кондиционирования воздуха и некоторых газопроводах.
Историческое развитие механики жидкостей шло двумя различными путями.
Первый путь — теоретический, путь точного математического анализа, основанного
на законах механики. Он привел
к созданию теоретической гидромеханики, которая долгое время являлась
самостоятельной дисциплиной, непосредственно не связанной с экспериментом.
Однако на пути чисто теоретического исследования движения жидкости встречается
множество трудностей, и методы теоретической гидромеханики не всегда
дают ответы па вопросы, выдвигаемые практикой.
Второй путь — путь широкого привлечения эксперимента и накопления опытных данных для использования их в инженерной практике — привел к созданию гидравлики; он возник из насущных задач практической, инженерной деятельности людей. В начальный период своего развития гидравлика была наукой чисто эмпирической. В настоящее время в ней, где это возможно и целесообразно, все больше применяют методы теоретической гидромеханики для решения отдельных задач, а теоретическая гидромеханика все чаще начинает прибегать к эксперименту как к критерию достоверности своих выводов. таким образом, различие в методах этих двух направлений одной и той же науки постепенно исчезает.
В настоящее время гидромеханика и гидравлика развиваются, как науки на пути сближения теоретических и экспериментальных знаний.
Методы, используемые в современной
гидравлике при исследовании движения, заключается в следующем.
1.Исследуемые явления сначала упрощают и к ним применяют законы теоретической механики.
2. Полученные результаты сравнивают с данными опытов, выясняют степень расхождения, уточняют и исправляют теоретические выводы и формулы для приспособления их к практическому использованию.
3. Явления трудно поддающихся теоретическому анализу из-за сложности, исследуют экспериментальным путем, а результаты представляют в виде эмпирических формул.
В результате разработаны методы расчета и проектирования разнообразных гидротехнических сооружений: плотин, каналов, водосливовов, трубопроводов, применяемых для подачи всевозможных жидкостей, а также для расчета гидромашин: насосов, гидротурбин, гидропередач, а также других гидравлических устройств.
Особенно велико значение гидравлики в машиностроении, где приходится иметь дело с закрытыми руслами (например, трубами) и напорными течениями в них, т. е. с потоками без свободной поверхности, когда давление в них отличается от атмосферного.
Гидросистемы, состоящие из насосов, трубопроводов, различных гидроагрегатов широко используют в машиностроении в качестве систем привода, систем охлаждения, систем топливоподачи, смазочных систем.
На различных современных машинах все в большом количестве применяются гидрогидромеханизмы и гидроавтоматика.
Гидромеханизмы представляют собой устройства для передачи механической энергии и преобразования движения с помощью жидкости. По сравнению с механизмами других видов, например, зубчатыми гидромеханизмы имеют ряд существенных преимуществ: простота преобразования вращательного движения в возвратно-поступательное, возможность плавного изменения скоростей входного и выходного звеньев, компактность конструкций малая удельная масса гидромашин при заданной мощности в сравнении с электромашинами.
Гидромеханизмы с системами автоматического или ручного управления, образуют гидроприводы, которые широко используют в металлообрабатывающих станках, на летательных аппаратах (самолетах, вертолетах, ракетах), на транспортных машинах (колесных и гусеничных), строительно-дорожных и подъемно-транспортных машинах, в прокатных станах и прессах.
Для расчета и проектирования гидроприводов и систем автоматического регулирования и других устройств с гидромашинами и гидроавтоматикой, а также для правильной их эксплуатации, ремонта и наладки нужно иметь соответствующую подготовку в области гидравлики и теории гидромашин.
1.3.
Силы, действующие на жидкость. Давление жидкости.
Жидкость в гидравлике рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т. е. отвлекаются от молекулярного строения жидкости и ее частицы даже малые, считают состоящими из большого числа молекул.
Вследствие текучести (подвижности частиц) в жидкости действуют силы не сосредоточенные, а непрерывно распределенные по ее объему (массе) или поверхности.
Внешние силы,
действующие на жидкость разделяют на
массовые (объемные) и поверхностные.
Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, для однородной жидкости, ее объему. К ним относятся сила тяжести и силы инерции переносного движения, действующая на жидкость при относительном ее покое в ускоренно движущихся сосудах или при относительном движении жидкости в руслах, перемещающихся с ускорением.
Поделив массовую силу на массу,
в правой части закона Ньютона получим ускорение равное единичной
массовой силе.
Поверхностные силы непрерывно, распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности. Эти силы обусловлены непосредственным воздействием соседних объемов жидкости на данный объем или же воздействием других тел (твердых или газообразных), соприкасающихся с данной жидкостью. Как следует из третьего закона Ньютона, с такими же силами, но в противоположном направлении, жидкость действует на соседние с нею тела.
В общем случае поверхностная сила ΔR, действующая па площадке ΔS , направлена под некоторым углом к ней, и ее можно разложить на нормальную ΔF и тангенциальную ΔТ составляющие (рис. 1.8). Первая называется силой давления, а вторая - силой трения.
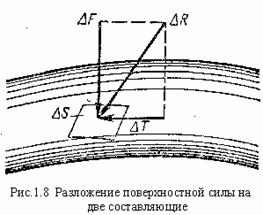
Если взять отношение поверхностной силы к площади,на которую она действует получим напряжение поверхностной силы, которое можно разложить
на нормальное и касательное напряжения.
1.Напряжение силы давления при движении жидкости, называется гидродинамическим давлением, в случае покоя — гидростатическим или просто давлением, и обозначается буквой Р.
Если сила давления ΔF равномерно распределена по площадке ΔS то, среднее давление определяют по формуле
Р= ΔF / ΔS. (2.1)
В общем случае давление в данной точке равно пределу, к которому стремится отношение силы давления ΔF к площади ΔS, на которую она действует, при стремлении ΔS к нулю.
Р
= lim ΔF /
ΔS (2.2)
ΔS→0
Если давление отсчитывают от абсолютного нуля то, его называют абсолютным, если отсчитывают от атмосферного давления Ра, то его называют избыточным Ризб или манометрическим. Следовательно, абсолютное давление
Рабс = Рат
+Ризб
Вакуумом или разряжением называется недостаток давления до атмосферного, который определяется, как разность между атмосферным давлением и абсолютным, если последнее меньше атмосферного.
Рвак = Рат
- Рабс
За единицу давления в Международной системе единиц (СИ) принят Паскаль — давление, вызываемое силой в один Ньютон, равномерно действующей на нормальной к этой силе поверхности площадью один метр квадратный. Применяют и укрупненные единицы: килопаскаль (кПа) и мегапаскаль (МПа):
1 Па=1 Н/м2=10-3 кПа=10-6 МПа.
В технике в настоящее время продолжают применять систему единиц МКГСС (метр, килограмм-сила, секунда), в которой за единицу давления принимается 1 кГс/см2, эта величина получила название техническая атмосфера, применяют также давление, измеренное в барах, обозначается, как 1 ат.
1 Па = 0,102*10-4 = кГс/см2.
Также используется система физических величин СГС (сантиметр, грамм-массы, секунда). В СГС сила является производной величиной, для ее определения используется закон второй Ньютона
F = m*a = 1 г*1 см/с2 = 1 г*(см/с2)/с2 = 1 дина(дин).
1 дин = 1—5 Н.
Соответственно в СГС применяются единицы давления при действии силды в 1 дин на 1 см2 площади. Соотношение между единицами давления в СГС и СИ
1 дин/см2 = 0,1 Па.
Бар (по гречески — тяжесть), внесистемная единица измерения давления, примерно равная одной атмосфере.
1 ат = 1 кГс/см2 = 10000 кГс/м2
1 бар = 105 Па=1,02 ат.
Существует еще понятие физическая атмосфера, равное 1,033 кГс/см2 . Соответствует нормальному атмосферному давлению на уровне моря. Значение атмосферного давления зависит от высоты над уровнем моря и от состояния атмосферы, физическая атмосфера обозначается, как 1 атм.
1 атм =9,87*10−6
Соотношение между единицами давления в системах СИ и МКГСС следующее:
1 Па=0,102 кГс/м2 или 1 кГс/м2= 9,81 Па≈10 Па.
Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой τ и выражается подобно давлению пределом
τ = lim ΔT
/ ΔS (1.3)
ΔS→0
а размерность его та же, что и размерность давления.
1.4.
Примеры гидравлических систем.
Структура агрегатов: энергосиловая, управляющая и информационная часть.
В качестве примера рассмотрим гидросистему экскаватора с гидравлическим приводом.
К энергосиловой части относится насосная установка, исполнительные механизмы, вторичная и первичная клапанная аппаратура.
К управляющей части относится гидрораспределители, система сервоуправления.
К информационной части относятся устройства отображения информации, манометрические точки, приборы контроля работы двигателя.
В насосную установку входят: двигатель, насос и система управления насосом. Исполнительные механизмы, состоят из гидроцилиндров, связанных с рычажными механизмами, гидромоторов с редукторами.
Гидрораспределители служат для направления и распределения рабочей жидкости от насоса, системы управления гидрораспределителями бывают механические (ручные), гидравлические, электрические и дистанционные.
Примеры использования гидравлических и пневматических систем.
1. Гидропривод экскаватора.
2. Пневмопривод тормозной системы автомобиля
3. Пневмосистема подкачки воздуха в бак подводной строительно-дорожной машины.
Рекомендуемая
литература.
1. Некрасов Б. Б.,Руднев, О. В. Байбаковым, Кирилловским Ю.Л, Башта Машиностроительная гидравлика.
2. Башта
Т.М. Машиностроительная гидравлика. М., Машиностроение,
3. Лабораторный
курс гидравлики, насосов и гидропередач. Под ред. С.С.Руднева и Л.Г.Подвиза.
–М., Машиностроение,
4. Некрасов
Б.Б. Гидравлика и ее применение на летательных аппаратах. – М.. машиностроение,
5. Д.А.Бутаев
и др. Сборник задач по машиностроительной гидравлике. Под ред. И.И.Куколевского
и Л.Г.Подвиза.-М., Машиностроение,
6. Френкель
Н.З. Гидравлика. – М.,Л., ГЭИ,