47) Погрешности измерения. Классификация составляющих погрешности измерения по причинам их возникновения.

Погрешность измерения.

При анализе измерений разграничиваются 2 понятия: истинное значение величины и результатом измерения.

Точность измерений характеризуются погрешностью измерения

                                   Аu=Lизм-Lист

На практике, вместо истинного значения используют так называемое действительное значение, т.е. значение найденное измерением с точностью примерно на порядок выше точности оцениваемого результата.

Du=Lизм-Lдейств

 

 

 

 

Погрешность измерения не равна погрешности средства измерения.

Классификация погрешностей по причинам возникновения.

 

 

 

 

 

 

Инструментальная погрешность (погрешность применяемого средства измерения) зависит от погрешностей средства измерения.

Причины возникновения несовершенство конструкции, неточность изготовления, погрешность градуирования и т.п.

В техническом паспорте указывается предел допускаемой погрешности при которой может быть использован прибор.

Различают основную и дополнительную погрешность средства измерения.

Основная погрешность - погрешность средства измерения, используемого в нормальных условиях.

Дополнительня погрешность - складывается из дополнительных погрешностей измерительного преобразователя и меры, вызванного отклонением от нормальных условий. Например, температура меры отличается от нормальной - это приведет к погрешности настройки прибора на нуль и соответствующей погрешности измерения.

Методическая погрешность - отражает несовершенство или упрощение методики измерения (отличие реальной схемы от теоретической).

При измерении размеров не жестких деталей прибором с большим измерительным усилием (проводятся бесконтактные измерения)

 

Субъективные (личные) погрешности возникают из-за индивидуальных особенностей оператора.

Погрешность установа Ay - связана с установкой объекта на приборе.

Погрешность отсчитывания D_ОТС

Погрешность параллакса - кажущееся смещение указателя

Погрешность интерполяции - недостаточно точное оценивание на глаз доли деления шкалы.  Для устранения применяют зеркальные шкалы. Стрелка должна быть совмещена с ее отражением в зеркале.

Основная и дополнительная погрешности.

Основная погрешность - определенная при нормальных условиях (температуре, давлении, влажности).

Дополнительная погрешность - возникает из-за отличия условий измерения от нормальных.

 

47) Случайные погрешности измерения и их оценка.

Классификация погрешностей по свойствам

 

 

 

D_И=D_СИСТ+D_СЛУЧ+D_ГР

 

 

Случайная погрешность - погрешность, изменяющая величину и знак от измерения к измерению случайных обстоятельств.

Систематическая погрешность - погрешность постоянная по определенному закону при повторных применениях

Грубая погрешность - возникает вследствие ошибки оператора или сбоя оборудования.

 

Если повторять измерения они будут отличными.

Вероятность ошибки отрицательная и положительная одинакова.

 

 

 

Оценка случайных погрешностей

Случайные погрешности трудно устранить. Они проявляются в рассеивании результатов многократных измерений одной и той же величины.

Оценку случайных погрешностей производят с помощью теории вероятности и математической статистики.

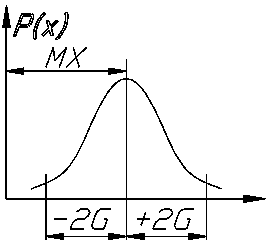
Нормальный закон распределения (закон Гаусса)

Этот закон является одним из наиболее распространенных законов распределения погрешностей, что объясняется центральной предельной теоремой теории вероятностей.

Центральная предельная теорема ТВ - распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа неравномерно действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Пример:

1. равноценные (50х50)

2. неравноценные (если событий >5)

3. незначительные по сравнению с сумарным действием.

 

Закон Гаусса имеет следующее выражения:

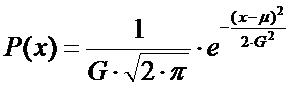
MX - математическое ожидание, оно является центром группирования результатов наблюдения.

G - среднеквадратичное отклонение характеризует величину рассеивания результатов наблюдений, т.е. точность измерения.

Дисперсия – математическое ожидание квадрата отклонения случайной величины от квадрата ее математического ожидания.

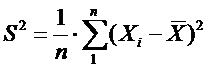 - смещенная характеристика дисперсии.

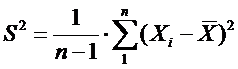- несмещенная характеристика дисперсии.

Так как среднее арифметическое  вычисляется по результатам отдельных наблюдений, то  является тоже случайной величиной и характеризуется своим эмпирическим средне квадратическим отклонением

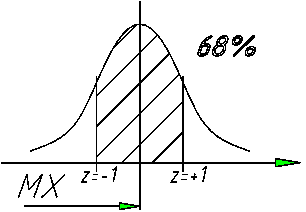68% - доверительная вероятность в этом интервале лежат 68% всех размеров, среднеквадратическое отклонение является 68% или доверительным интервалом.

 

 

 

 

 

95% - в промышленности               99.73% - в научных исследованиях

Доверительный интервал, интервал в котором мы ожидаем размер.

Доверительная вероятность - вероятность того, что размеры деталей или результаты измерения окажется внутри доверительного интервала.

За оценку случайной погрешности результата измерений принимают доверительный интервал среднего арифметического.

Случайные погрешности, > 3G , считаются грубыми и исключаются из результата  измерения.

При малом n используют коэффициент Стьюдента, где

При n®¥ распределение Стьюдента переходит в нормальное распределение, чем больше n, тем меньше коэф. Стьюдента, интервал с заданной вероятностью уменьшается

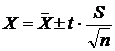,     P=       , n=